slam
Robust Initialization of VINS
T. Qin and S. Shen, “Robust initialization of monocular visual-inertial estimation on aerial robots,” in 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) , Vancouver, BC: IEEE, Sep. 2017, pp. 4225–4232. doi: 10.1109/IROS.2017.8206284 .
这篇文章提出了一种鲁棒的视觉惯性系统初始化方法,通过松耦合的方式对齐 IMU 与视觉数据,主要解决了外参数标定、陀螺仪偏置估计、速度重力尺度和视觉惯性对齐等关键问题。
问题建模
IMU 测量模型有
\[
\begin{aligned}
\hat{\boldsymbol\omega} &= \boldsymbol\omega^b+\mathbf b^g+\mathbf n^g \\
\hat{\mathbf a} &= \mathbf R_{bw}(\mathbf a^w+\mathbf g^w)+\mathbf b^a+\mathbf n^a
\end{aligned}
\]
预积分
\[
\begin{aligned}
\boldsymbol\alpha_{b_ib_j}&=\iint_{t \in [i,j]} \mathbf R_{b_ib_t} (\hat{\mathbf a}^{b_t}-\mathbf b^a) {\rm d} t^2\\
\boldsymbol\beta_{b_ib_j} &= \int_{t \in [i,j]} \mathbf R_{b_ib_t} (\hat{\mathbf a}^{b_t}-\mathbf b^a) {\rm d} t \\
\mathbf q_{b_ib_j}&= \int_{t \in [i,j]} \mathbf q_{b_ib_t} \otimes \begin{bmatrix} 0 \\ \frac12(\hat{\boldsymbol\omega}^{b_t}-\mathbf b^g) \end{bmatrix} {\rm d}t
\end{aligned}
\]
有一阶泰勒展开近似
\[
\begin{aligned}
\boldsymbol\alpha_{b_ib_j} &\approx \hat{\boldsymbol\alpha}_{b_ib_j} + \mathbf J_{b^a}^\alpha\delta\mathbf b^a + \mathbf J_{b^g}^\alpha\delta\mathbf b^g \\
\boldsymbol\beta_{b_ib_j} &\approx \hat{\boldsymbol\beta}_{b_ib_j} + \mathbf J_{b^a}^\beta\delta\mathbf b^a + \mathbf J_{b^g}^\beta\delta\mathbf b^g \\
\mathbf q_{b_kb_{k+1}} &\approx \hat{\mathbf q}_{b_kb_{k+1}}\otimes\begin{bmatrix}1\\\frac12\mathbf J_{b^g}^{\mathbf q}\delta\mathbf b^g\end{bmatrix}
\end{aligned}
\]
SfM 给出视觉约束,\(\bar ·\) 表示非米制单位
\[
\begin{aligned}
\mathbf q_{c_0b_k} &= \mathbf q_{c_0c_k} \otimes \mathbf q_{bc}^{-1} \\
s\bar{\mathbf p}_{c_0b_k} &= s\bar{\mathbf p}_{c_0c_k} - \mathbf R_{c_0b_k}\mathbf p_{bc}
\end{aligned}
\]
估计外参数 \(\mathbf q_{bc}\)
对于相邻时刻 \(k,k+1\) 的 IMU 旋转积分 \(\mathbf q_{b_kb_{k+1}}\) 和视觉测量 \(\mathbf q_{c_kc_{k+1}}\)
\[
\mathbf q_{b_kc_{k+1}}=\mathbf q_{bc}\otimes\mathbf q_{c_kc_{k+1}}=\mathbf q_{b_kb_{k+1}}\otimes\mathbf q_{bc}
\]
\[
\left([\mathbf q_{c_kc_{k+1}}]_R - [\mathbf q_{b_kb_{k+1}}]_L\right)\mathbf q_{bc}=\mathbf0
\]
\([·]_L, [·]_R\) 为四元数的左乘矩阵和右乘矩阵,\([·]_\times\) 为反对称矩阵
\[
\begin{aligned}\
[\mathbf q]_L &=q_\omega\mathbf I+\begin{bmatrix}0 & -\mathbf q_v^T \\ \mathbf q_v & [\mathbf q_v]_\times\end{bmatrix} \\
[\mathbf q]_R &= q_\omega\mathbf I+\begin{bmatrix}0 & -\mathbf q_v^T \\ \mathbf q_v & -[\mathbf q_v]_\times\end{bmatrix} \\
[\boldsymbol\omega]_\times &= \begin{bmatrix}0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0\end{bmatrix}
\end{aligned}
\]
将多个时刻的 IMU 预积分和视觉测量累计,即可得到关于 \(\mathbf q_{bc}\) 的超定方程组
\[
\begin{bmatrix}
[\mathbf q_{c_0c_1}]_R-[\mathbf q_{b_0b_1}]_L \\
[\mathbf q_{c_1c_2}]_R-[\mathbf q_{b_1b_2}]_L \\
\vdots \\
[\mathbf q_{c_nc_{n-1}}]_R-[\mathbf q_{b_nb_{n-1}}] \\
\end{bmatrix} \mathbf q_{bc} = \mathbf 0
\]
利用奇异值分解可解得 \(\mathbf q_{bc}\)
估计陀螺仪偏置
标定得到 \(\mathbf q_{bc}\) 后,利用旋转约束,可估计处陀螺仪偏置
\[
\delta\mathbf b^g = \arg\min_{\delta\mathbf b^g}\sum_{k\in{\mathcal B}} \left|\left|\left\lfloor\mathbf q_{c_0b_{k+1}}^{-1}\otimes\mathbf q_{c_0b_k} \otimes\mathbf q_{b_kb_{k+1}} \right\rfloor_{\text{xyz}}\right|\right|^2
\]
\(\mathcal B\) 为所有关键帧的集合,其中目标函数取最小值 \(0\) 时
\[
\mathbf q_{c_0b_{k+1}}^{-1}\otimes\mathbf q_{c_0b_k} \otimes\mathbf q_{b_kb_{k+1}}=\begin{bmatrix}1\\\mathbf0\end{bmatrix}
\]
又由旋转预积分一阶泰勒近似
\[
\mathbf q_{b_kb_{k+1}} \approx \hat{\mathbf q}_{b_kb_{k+1}}\otimes\begin{bmatrix}1\\\frac12\mathbf J_{b^g}^{\mathbf q}\delta\mathbf b^g\end{bmatrix}
\]
联立得到
\[
\begin{bmatrix}1\\\frac12\mathbf J_{b^g}^{\mathbf q}\delta\mathbf b^g\end{bmatrix} = \hat{\mathbf q}_{b_kb_{k+1}}^{-1}\otimes\mathbf q_{c_0b_k}^{-1}\otimes\mathbf q_{c_0b_{k+1}}
\]
考虑虚部
\[
\mathbf J_{b^g}^{\mathbf q}\delta\mathbf b^g = 2\left\lfloor\hat{\mathbf q}_{b_kb_{k+1}}^{-1}\otimes\mathbf q_{c_0b_k}^{-1}\otimes\mathbf q_{c_0b_{k+1}}\right\rfloor_{\text{xyz}}
\]
进一步可以构建正定方程组,通过 Cholesky 分解求解 \(\delta\mathbf b^g\)
\[
(\mathbf J_{b^g}^{\mathbf q})^T\mathbf J_{b^g}^{\mathbf q}\delta\mathbf b^g = 2(\mathbf J_{b^g}^{\mathbf q})^T\left\lfloor\hat{\mathbf q}_{b_kb_{k+1}}^{-1}\otimes\mathbf q_{c_0b_k}^{-1}\otimes\mathbf q_{c_0b_{k+1}}\right\rfloor_{\text{xyz}}
\]
解得 \(\delta\mathbf b^g\) 后,重新计算预积分项 \(\hat{\boldsymbol\alpha}_{b_kb_k+1}, \hat{\boldsymbol\beta}_{b_kb_{k+1}},\hat{\mathbf q}_{b_kb_{k+1}}\)
初始化速度、重力和尺度因子
所有我们希望估计的变量包括
\[
\mathcal X_I=\begin{bmatrix}\mathbf v_0^{b_0} & \mathbf v_1^{b_1} & \cdots \mathbf v_n^{b_n} & \mathbf g^{c_0} & \mathbf s\end{bmatrix}^T
\]
由 \(1.3\) 式和 \(2.1\) 式,得到
\[
\begin{aligned}
& \boldsymbol\alpha_{b_kb_{k+1}} = \mathbf R_{b_kc_0} \left( s(\bar{\mathbf p}_{c_0b_{k+1}} - \bar{\mathbf p}_{c_0b_k}) + \frac12\mathbf g^{c_0}\Delta t_k^2 - \mathbf R_{c_0b_k}\mathbf v_{k}^{b_k} \Delta t_k \right) \\
& \boldsymbol\beta_{b_kb_{k+1}} = \mathbf R_{b_kc_0} (\mathbf R_{c_0b_{k+1}}\mathbf v_k^{b_k}+\mathbf g^{c_0}\Delta t_k - \mathbf R_{c_0b_k}\mathbf v_k^{b_k})
\end{aligned}
\]
整理方程得到
\[
\hat{\mathbf z}_{b_{k+1}}^{b_k} = \begin{bmatrix} \hat{\boldsymbol\alpha}_{b_kb_{k+1}} - \mathbf p_{bc} + \mathbf R_{b_kc_0}\mathbf R_{c_0b_{k+1}}\mathbf p_{bc} \\ \hat{\boldsymbol\beta}_{b_kb_{k+1}} \end{bmatrix} = \mathbf H^k\mathcal X_I^k+\mathbf n^k
\]
其中
\[
\begin{aligned}
\mathcal X_I^k &= \begin{bmatrix} \mathbf v^{b_k}_k & \mathbf v^{b_{k+1}}_{k+1} & \mathbf g^{c_0} & s \end{bmatrix}^T \\
\mathbf H_{b_{k+1}}^{b_k} &= \begin{bmatrix} -\mathbf I\Delta t_k & \mathbf0 & \frac12\mathbf R_{b_kc_0}\Delta t_k^2 & \mathbf R_{b_kc_0}(\bar{\mathbf p}_{c_0b_{k+1}} - \bar{\mathbf p}_{c_0b_k}) \\ -\mathbf I & \mathbf R_{b_kc_0}\mathbf R_{c_0b_{k+1}} & \mathbf R_{b_kc_0}\Delta t_k & 0 \end{bmatrix}
\end{aligned}
\]
进而可以转化为最小二乘问题求解
\[
\mathcal X_I=\arg\min_{\mathcal X_I}\sum_{k\in\mathcal B}||\hat{\mathbf z}_{b_{k+1}}^{b_k} - \mathbf H_{b_{k+1}}^{b_k}\mathcal X_I^k||^2
\]
同样可以通过 Chologky 分解求得
重力向量优化
在重力模长已知的情况下,重力向量实际自由度为 \(2\) ,可以利用球面坐标进行参数化
\[
\hat{\mathbf g}^{c_0}=||g||\bigg(\frac{\tilde{\mathbf g}^{c_0}}{||\tilde{\mathbf g}^{c_0}||}+w_1\mathbf b_1+w_2\mathbf b_2\bigg)
\]
\(\tilde{\mathbf g}^{c_0}\) 为 \(2.15\) 中求得的重力向量,记 \(\frac{\tilde{\mathbf g}^{c_0}}{||\tilde{\mathbf g}^{c_0}||}\) 为 \(\hat{\bar{\mathbf g}}^{c_0}\)
可以通过如下方式找到一组基底垂直于 \(\hat{\bar{\mathbf g}}^{c_0}\)
\[
\begin{aligned}
& \mathbf b_1 = \begin{cases}
\hat{\bar{\mathbf g}}^{c_0}\times[1,0,0]^T, &\hat{\bar{\mathbf g}}^{c_0}\ne[1,0,0]^T \\
\hat{\bar{\mathbf g}}^{c_0}\times[0,0,1]^T, &\text{otherwise}
\end{cases} \\
& \mathbf b_2 = \hat{\bar{\mathbf g}}^{c_0}\times \mathbf b_1
\end{aligned}
\]
将 \(2.17\) 式代入 \(2.15\) 式,得到
\[
\begin{aligned}
\mathcal X_I^k &= \begin{bmatrix} \mathbf v^{b_k}_k & \mathbf v^{b_{k+1}}_{k+1} & \mathbf w^{c_0} & s \end{bmatrix}^T \\
\mathbf H_{b_{k+1}}^{b_k} &= \begin{bmatrix} -\mathbf I\Delta t_k & \mathbf0 & \frac12\mathbf R_{b_kc_0}\begin{bmatrix}\mathbf b_1^T\\\mathbf b_2^T\end{bmatrix}\Delta t_k^2 & \mathbf R_{b_kc_0}(\bar{\mathbf p}_{c_0b_{k+1}} - \bar{\mathbf p}_{c_0b_k}) \\ -\mathbf I & \mathbf R_{b_kc_0}\mathbf R_{c_0b_{k+1}} & \mathbf R_{b_kc_0}\begin{bmatrix}\mathbf b_1^T\\\mathbf b_2^T\end{bmatrix}\Delta t_k & 0 \end{bmatrix}
\end{aligned}
\]
观测方程变为
\[
\hat{\mathbf z}_{b_{k+1}}^{b_k} = \begin{bmatrix} \hat{\boldsymbol\alpha}_{b_kb_{k+1}} - \mathbf p_{bc} + \mathbf R_{b_kc_0}\mathbf R_{c_0b_{k+1}}\mathbf p_{bc}-\frac12\mathbf R_{b_kc_0}\tilde{\mathbf g}^{c_0}\Delta t_k^2 \\ \hat{\boldsymbol\beta}_{b_kb_{k+1}} -\mathbf R_{b_kc_0}\tilde{\mathbf g}^{c_0}\Delta t_k \end{bmatrix}
\]
利用最小二乘对 \(\mathcal X_I^k\) 进一步优化
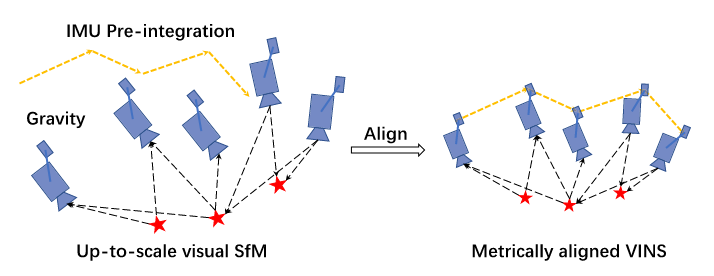
视觉惯性对齐
根据旋转的性质和李代数的指数映射,我们可以构建从 \(c_0\) 系到 \(w\) 系的旋转矩阵 \(\mathbf R_{wc_0}\)
\[
\mathbf R_{wc_0}=\exp\bigg[\arctan\left(\frac{||\hat{\mathbf g}^{c_0}\times\hat{\mathbf g}^{w}||}{\hat{\mathbf g}^{c_0}\cdot\hat{\mathbf g}^{w}}\right)\cdot\frac{\hat{\mathbf g}^{c_0}\times\hat{\mathbf g}^{w}}{||\hat{\mathbf g}^{c_0}\times\hat{\mathbf g}^{w}||}\bigg]
\]
接着为所有 \(c_0\) 系为坐标系的向量左乘 \(\mathbf R_{wc_0}\) ,同时将非米制的 \(\bar{\mathbf p}\) 通过尺度因子 \(s\) 恢复为 \(\mathbf p\)
未估计的参数
作者通过实验指出二者加速度计偏置 \(\mathbf b^a\) 和相机与 IMU 间的平移向量 \(\mathbf p_{bc}\) 对系统精度影响极小,可以不在初始化中显式优化